(#4) Le théorème des 4 couleurs - YouTube
Bonjour à tous, aujourd'hui on va parler coloriage, géographie et mathématiques
avec le théorème des quatre couleurs.
Le théorème des quatre couleurs c'est un de mes théorèmes préférés.
C'est un théorème qui dit que si vous prenez une carte géographique,
qui contient des pays ou des régions,
vous pouvez toujours la colorier en utilisant seulement quatre couleurs.
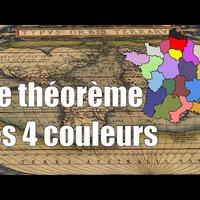
Par exemple, ici, j'ai pris l'exemple de la carte des régions françaises
et je l'ai coloriée en utilisant seulement rouge, vert, jaune et bleu.
J'ai pris les régions actuelles mais j'aurais très bien pu prendre les régions futures,
ou en fait n'importe quelle carte, ça marche aussi.
Là, vous allez me dire, si on veut on peut très bien la colorier en utilisant une seule couleur.
Oui, évidemment vous pouvez toujours utiliser une seule couleur.
Mais si vous faites ça, vous violez la règle fondamentale
qui est que quand on a deux régions ou deux pays qui se touchent,
on veut utiliser deux couleurs différentes, sinon on ne voit pas la frontière
Alors en pratique, les gens qui font des cartes utilisent six couleurs, sept couleurs voire plus.
Mais ce que dit ce théorème, c'est qu'on peut toujours trouver un moyen de colorier
en n'utilisant que quatre couleurs.
Moi, la première fois que j'ai entendu parler de ce théorème, je trouvais ça un peu incroyable.
Je me disais, quatre couleurs c'est pas assez,
on doit pouvoir trouver un contre-exemple, il suffit de faire une carte complètement alambiquée
avec des pays tordus.
Et je dois avouer que j'ai passé quelques cours de philo à jouer avec mon voisin
à essayer de trouver un contre-exemple au théorème des quatre couleurs.
Le principe du jeu est simple,
l'un des deux dessine une carte complètement alambiquée avec des régions tordues
qui se touchent les unes les autres.
Il passe la carte à l'autre qui essaye de la colorier en utilisant seulement quatre couleurs.
Et s'il arrive à la colorier, c'est que ce n'était pas un contre-exemple.
Evidemment c'était un jeu complètement vain puisque je vous ai dit:
le théorème des quatre couleurs, c'est un théorème.
Un théorème ça veut dire qu'il n'y a pas de contre-exemple donc ça ne sert à rien d'en chercher un.
Ce qu'il faut savoir sur ce théorème, c'est qu'il a un statut particulier dans le cœur des mathématiciens.
C'est un théorème qui a l'air simple, on se dit, la démonstration elle est peut-être facile.
En fait elle n'est pas facile du tout, elle est même très difficile.
A tel point que les premiers qui ont réussi à le démontrer, c'était seulement dans les années 70,
ils ont dû s'aider d'un ordinateur et c'était quelque chose de complètement nouveau.
D'habitude quand on fait une démonstration en maths on prend son papier, son crayon,
ou alors son tableau et sa craie.
Et on écrit son raisonnement, des fois ça prend trois lignes, des fois ça prend 300 pages,
mais à la fin on peut tout écrire à la main.
Dans le cas de la démonstration du théorème des quatre couleurs,
il y avait plus de 1900 cas différents à traiter à la main
et les deux qui ont fait ça, s'ils avaient voulu le faire vraiment à la main, ils y auraient passé toute leur vie.
Donc ils ont tout rentré dans un ordinateur et ils ont laissé l'ordinateur faire les vérifications.
Et quand l'ordinateur a eu fini, ils ont considéré que le théorème était démontré.
Et ça, ça a causé beaucoup de débats parmi les mathématiciens,
car il y en a qui considéraient qu'utiliser un ordinateur pour faire une démonstration c'était pas valide.
Comment on est sûrs que le programme tourne correctement?
Comment on est sûrs que l'ordinateur ne fait pas d'erreur, qu'il n'y a pas un bug,
qu'il n'y a pas un court-circuit, un problème de mémoire, n'importe quoi?
Donc, ils ont dit non, cette démonstration là elle n'est pas valide.
Depuis ça a été beaucoup amélioré et on a vraiment une totale confiance dans la démonstration du théorème des quatre couleurs
et depuis il y a eu d'autres théorèmes qui ont été montrés par ordinateur.
Mais il reste encore chez les matheux quelques irréductibles qui considèrent
que ce n'est pas des démonstrations valides
et qu'il faut continuer à chercher une démonstration du théorème des quatre couleurs
qui puisse se faire entièrement à la main.
Si malgré ce que je vous ai dit, vous persistez à vouloir vous aussi essayer de trouver
un contre-exemple au théorème des quatre couleurs,
il faut que vous sachiez qu'il y a deux conditions pour qu'il soit valide.
La première condition c'est qu'on veut que les pays ou les régions ne soient que d'un seul tenant, d'un seul morceau
On ne veut pas, par exemple, un pays qui serait coupé en deux morceaux déconnectés.
En mathématiques ont dit qu'on veut que les pays soient connexes.
Alors, en pratique, cette condition elle n'est à-peu-près jamais vérifiée.
Prenez simplement l'exemple des îles, une île elle est forcément déconnectée du continent
et donc on a une situation d'un pays qui est en deux morceaux.
En pratique les îles ne posent pas trop de problèmes pour quand même colorier avec quatre couleurs,
mais il y a des cas qui sont un peu plus tordus.
Il y a par exemple un exemple fameux, c'est l'enclave de Kaliningrad. L'enclave de Kaliningrad c'est un petit morceau de la Russie qui est déconnecté
de la partie principale de la Russie
et qui est coincé entre la Lituanie, la Mer Baltique et la Pologne.
Alors, un cas comme l'enclave de Kaliningrad, ce n'est pas trop problématique,
on peut quand même, probablement colorier la région avec seulement quatre couleurs.
Mais si vous commencez à imaginer que tous les pays ont des enclaves les uns dans les autres,
là c'est facile de se convaincre que le théorème des quatre couleurs ne marche plus.
Et d'ailleurs, cette situation là, elle existe.
Parce que si vous réfléchissez bien, c'est exactement ce qui se passe avec les ambassades.
Vous savez, une ambassade elle fait partie du territoire national.
Par exemple, l'ambassade d'Allemagne à Paris, c'est un morceau de l'Allemagne.
Donc avec toutes les ambassades qu'il y a dans tous les pays,
on a vraiment cette situation où tous les pays ont des enclaves les uns dans les autres
et si on voulait colorier aussi les ambassades, avec quatre couleurs ça ne suffirait pas.
L'autre condition à respecter pour que le théorème des quatre couleurs soit valide,
c'est qu'on ne veut pas que sur notre carte il y ait des points où plus de trois pays se rencontrent.
Un cas où trois pays se rencontrent, c'est le cas normal,
quand vous avez deux frontières, vous avez trois pays qui se touchent sur un seul point.
Mais on interdit qu'il y ait quatre voire cinq pays, ou plus, qui se touchent au même point.
C'est assez facile à comprendre, si vous imaginez que vous avez cinq pays qui se touchent en un seul point,
chaque pays est en contact avec les quatre autres et donc, il faudra au moins cinq couleurs pour les colorier.
Je me suis demandé si ce genre de situation existait entre les pays.
Alors en fait, à l'heure actuelle, ça n'existe pas, mais ça a existé notamment dans les années 60 en Afrique.
A un moment donné il y avait une situation où on avait la Zambie, le Zimbabwe, la Namibie et le Botswana
qui se touchaient tous les quatre en un seul point.
Alors ça n'a pas duré très longtemps parce que ça posait quand même quelques petits problèmes.
Notamment, si vous avez une situation comme ça, ça veut dire qu'en principe
les gens qui sont dans le pays du Nord peuvent aller directement dans le pays du Sud
sans passer, ni par celui de l'Est, ni par celui de l'Ouest.
Ce qui ne pose pas forcement trop de problèmes quand c'est juste des gens,
mais si ça commence à être des troupes, là ça cause des petits soucis géopolitiques.
En fait, cette situation n'a pas duré très longtemps
et rapidement c'est revenu à une situation normale où on avait seulement que trois pays qui se touchaient.
Au niveau international, aujourd'hui ça n'existe plus mais on trouve pas mal de cas au niveau national.
Il y a un exemple très connu qui est aux Etats-Unis,
il y a un endroit où on a quatre états qui se touchent, qui se rencontrent à angle droit.
C'est l'Utah, le Colorado, l'Arizona et le Nouveau Mexique.
Et les Américains se sont même amusés à construire un petit monument à cet endroit là
et dans le sol, il y a même une toute petite plaque qui indique le point exact où les quatre états se rencontrent.
Donc sur la photo que vous voyez là, le petit garçon est dans quatre états différents à la fois.
Il y a même des cartes encore plus tordues, le plus tordu que j'ai trouvé ça se passe autour de l'Etna en Sicile.
Autour de l'Etna il y a dix communes différentes
et administrativement ces dix communes se rencontrent toutes au sommet de l'Etna.
Donc, si cette région vous vouliez la colorier avec des couleurs différentes pour chaque communes,
vous seriez obligés d'utiliser au moins dix couleurs.
Donc ça veut dire aussi que si vous vous tenez au sommet de l'Etna, exactement,
vous êtes dans dix communes différentes à la fois.
Ceci dit, je vous déconseille de vous tenir au sommet de l'Etna.
Pour conclure, sachez que le théorème des quatre couleurs n'a strictement aucun intérêt pratique.
En général, les gens qui font des cartes ne sont pas rationnés en nombre de couleurs.
Le théorème des quatre couleurs intéresse juste les mathématiciens
et les gens comme moi qui ont des théorèmes préférés.
Merci d'avoir suivi cette vidéo, n'oubliez pas de la partager.
Vous pouvez aussi aller voir mes vidéos précédentes, vous abonner à la chaîne
et me retrouver sur mon blog "Science Étonnante".
Vous pouvez aussi me suivre sur Facebook et sur Twitter. A bientôt!
Sous-titres: Warteks