Μαθηματικά | Θυμάμαι τους δεκαδικούς αριθμούς | Δ΄Δημοτικού Επ. 46
Καλημέρα, παιδιά!
Είμαι η Κατερίνα Παινέση και σήμερα θα κάνουμε μαζί μαθηματικά.
Θα γνωρίσουμε τους δεκαδικούς αριθμούς.
Αν είστε τερατάκια... τεταρτάκια ήθελα να πω...
σίγουρα έχετε ακούσει τους δεκαδικούς αριθμούς, ήδη από την Γ' Δημοτικού.
Θα μου πείτε τώρα, τι τους θέλουμε τους δεκαδικούς;
Είναι εκεί μες στα βιβλία των μαθηματικών και μας βασανίζουν.
Σας πληροφορώ πως όχι. Οι δεκαδικοί αριθμοί βρίσκονται παντού γύρω μας.
Δεν είναι κάποιοι αριθμοί κλεισμένοι μέσα στα βιβλία, με μόνο σκοπό της ζωής τους να μας ταλαιπωρούν.
Από την πρώτη στιγμή που γεννιόμαστε ερχόμαστε σε επαφή με τους δεκαδικούς αριθμούς.
Δεν με πιστεύετε; Αλήθεια σας λέω!
Μόλις γεννηθήκατε, μια νοσοκόμα σας πήρε και έβαλε μια μεζούρα...
μια τέτοια μεζούρα, να μετρήσει το ύψος σας.
Κατέγραψε το ύψος σε αυτό εδώ το βιβλιάριο.
Έγραψε ας πούμε, ύψος: 0,51 μέτρα.
Μετά, σας πήρε και σας έβαλε σε μία ζυγαριά. Κατέγραψε το βάρος σας στο βιβλιάριο.
Πάλι χρησιμοποιώντας δεκαδικούς αριθμούς.
Βάρος: 3,150 κιλά.
Με τη μεζούρα μέτρησε την περίμετρο του κεφαλιού.
Περίμετρος κεφαλής: 0,35 μέτρα.
Κάθε φορά που πάτε στον παιδίατρο, αυτός σημειώνει πόσο ψηλώσατε και πόσο βάρος πήρατε.
Και τώρα που έχετε μεγαλώσει και έχετε φτάσει στην Δ' τάξη, είμαι σίγουρη ότι το βιβλιάριό σας γράφει...
ύψος: 1,40 μέτρα, βάρος: 30 κιλά. Και όλοι σας λένε: Πώς έχεις μεγαλώσει έτσι!
Και σίγουρα, αφού έχετε μεγαλώσει τόσο πολύ, βοηθάτε και τους γονείς σας στα ψώνια.
Πηγαίνετε λοιπόν στο σούπερ μάρκετ μαζί με τους γονείς σας, και... εκεί να δεις δεκαδικούς!
Χαμός γίνεται!
Όλες οι τιμές των προϊόντων, οι περισσότερες είναι σε δεκαδικούς αριθμούς.
Το βάρος τους, σε δεκαδικούς αριθμούς.
Πάμε να πληρώσουμε στο ταμείο. Πάλι με δεκαδικούς αριθμούς συννενοούμαστε...
γιατί τα νομίσματα μας σε δεκαδικούς αριθμούς τα έχουμε.
Πάμε λοιπόν να δούμε και να βοηθήσουμε τον φίλο μας τον Σαλ.
Τον ξέρετε τον Σαλ, από το βιβλίο των μαθηματικών.
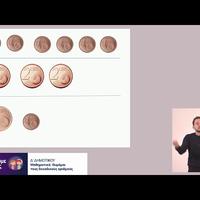
Ο Σαλ θέλει να αγοράσει αυτοκόλλητα.
Έχει βρει αυτές τις πολύ ωραίες καρτέλες με αυτοκόλλητα, που η καθεμία κοστίζει 1 ευρώ.
Η καρτέλα αυτή βλέπουμε ότι έχει πάρα πολλά αυτοκόλλητα.
Αν αρχίσουμε να τα μετράμε ένα - ένα, κάπου θα μπερδευτούμε, θα το χάσουμε, θα κάνουμε λάθος.
Αν παρατηρήσουμε την καρτέλα πιο προσεκτικά, θα δούμε ότι είναι χωρισμένη σε σειρές.
Κάθε σειρά έχει δέκα διαφορετικά αυτοκόλλητα.
Και κάθε στήλη έχει δέκα ίδια αυτοκόλλητα.
Ο Σαλ λοιπόν αγόρασε μια λωρίδα με αυτοκόλλητα, μια στήλη.
Ήθελε να πάρει τις μπάλες του μπάσκετ. Του αρέσει πάρα πολύ το μπασκετ, απ' ό,τι φαίνεται.
Μας λέει ότι πλήρωσε δίνοντας μόνο ένα κέρμα.
Ποιο κέρμα να ήταν αυτό;
Για να δούμε!
Όλη η καρτέλα κοστίζει 1 ευρώ. Άρα, αφού ο Σαλ αγόρασε το 1/10 της καρτέλας,
Αγόρασε το 1 κομμάτι από τα 10, δηλαδή το 1/10.
Ή 0,1 της καρτέλας.
Δεν μπορεί να έδωσε 1 ολόκληρο ευρώ.
1 ευρώ κάνει όλη η καρτέλα.
Πώς το χώρισε το 1 ευρώ, για να δώσει όσα λεφτά χρειαζόταν για να πάρει τα αυτοκόλλητα;
Το 1 ευρώ ξέρουμε ότι χωρίζεται σε μικρότερα νομίσματα, σε 100 λεπτά.
1 ευρώ έχει 100 λεπτά. Άρα για να δώσει το 1/10 των 100 λεπτών...
Πρέπει να έδωσε... 100/10 = 10 λεπτά.
Μας λέει ότι έδωσε μόνο 1 κέρμα, άρα έδωσε το κέρμα των 10 λεπτών.
Θα μπορούσε να έχει δώσει και 10 κέρματα του 1 λεπτού.
Όμως αφού μας λέει ότι έδωσε μόνο 1 κέρμα, έδωσε 1 κέρμα των 10 λεπτών.
Πάμε να δούμε τη φίλη μας την Ηρώ.
Η Ηρώ αγόρασε λίγα αυτοκόλλητα.
Ήταν πολύ επιλεκτική. Είχε λίγα χρήματα στο πορτοφολάκι της,
και λέει: θέλω να αγοράσω ένα αστεράκι, ένα σαλιγκάρι, ένα λουλουδάκι, ένα κοχύλι, ένα ψαράκι και μια φατσούλα.
6 αυτοκόλλητα, συνολικά.
6 από τα 100 αυτοκόλλητα της καρτέλας. 6/100.
Ή 0,06 της καρτέλας.
Θα πρέπει λοιπόν να πληρώσει με 6/100 του ευρώ.
Είπαμε το 1 λεπτό είναι 1/100 του ευρώ, άρα χρειάζεται 6 λεπτά η Ηρώ για να πληρώσει.
Με τι κέρματα μπορεί να πληρώσει; Μπορείτε να μου πείτε αμέσως, αμέσως, ότι μπορεί να πληρώσει...
με 6 κέρματα του 1 λεπτού.
Σωστά!
Κάποιος άλλος μπορεί να μου πει ότι μπορεί να δώσει 3 κέρματα των 2 λεπτών.
3 x 3 = 6. Άρα και αυτή η απάντηση είναι σωστή.
Μπορεί να έχει και κέρμα των 5 λεπτών μες στο πορτοφόλι της, και να βάλει 1 κέρμα των 5 λεπτών και 1 του 1 λεπτού.
Και να έχει 6 λεπτά να πληρώσει τα αυτοκόλλητα.
Υπάρχουν και άλλοι συνδυασμοί. Θα μπορούσε να βάλει 1 κέρμα των 2 λεπτών...
και 4 του 1 λεπτού.
Σίγουρα δεν θα μπορούσε να βάλει 2 κέρματα των 3 λεπτών, γιατί δεν έχουμε τέτοια κέρματα.
Ξέρετε ότι τα κέρματα, τα μικρά τα χάλκινα είναι του 1 λεπτού, των 2 ή των 5 λεπτών.
Μετά πάμε στα 10 λεπτά.
Για να δούμε τώρα τι μας λέει η Στέλλα.
Η Στέλλα δεν μας λέει πόσα αυτοκόλλητα αγόρασε, μας λέει μόνο πόσα χρήματα έδωσε.
Έδωσε 1, 23 ευρώ.
Τι μπορεί να αγόρασε;
Το τετράγωνο που βλέπετε εδώ, είναι τα αυτοκόλλητα που μπορεί να αγόρασε η Στέλλα.
Αφού έδωσε 1,23 ευρώ, σημαίνει ότι μπορεί να αγόρασε μια ολόκληρη καρτέλα.
Δεύτερη καρτέλα μπορεί να αγόρασε, άραγε;
Όχι. Αν ήθελε να αγοράσει και δεύτερη καρτέλα θα έπρεπε να έχει...
και δεύτερο ευρώ. Δεν έχει όμως, γιατί έχει δώσει 1,23 ευρώ.
Άρα αγόρασε μια καρτέλα και κάτι ακόμα.
Μια καρτέλα και...; Για να δω, θα το βρείτε;
Και 23 αυτοκόλλητα ακόμα.
23 αυτοκόλλητα που μπορεί να είναι σε 2 στήλες και 3 αυτοκόλλητα ξεχωριστά.
Έτσι έχει αγοράσει 1 καρτέλα, 2 λωρίδες και 3 αυτοκόλλητα που της άρεσαν, χώρια.
Έδωσε λοιπόν συνολικά 1,23 ευρώ.
Πάμε να δούμε τον αριθμό αυτό: 1,23.
Θυμάστε από πέρσι ότι οι δεκαδικοί αριθμοί έχουν ένα μικρό σημαδάκι.
Αυτό το μικρό σημαδάκι χωρίζει τον αριθμό.
Χωρίζει το ακέραιο μέρος...
από το δεκαδικό.
Ακέραιο σημαίνει ολόκληρο.
Είναι η ολόκληρη καρτέλα που αγόρασε η Στέλλα.
Είναι το ολόκληρο ευρώ που έδωσε.
Είναι οι μονάδες που ξέρουμε, στην προκειμένη περίπτωση.
Δεξιά από την υποδιαστολή, από το κόμμα, το πρώτο ψηφίο είναι τα δέκατα.
2 δέκατα έχει αυτός ο αριθμός.
Είναι οι δυο λωρίδες που είχαν η καθεμία από 10 αυτοκολλητάκια.
Ενώ το 3, ο δεύτερος αριθμός μετά την υποδιαστολή, είναι τα εκατοστά.
Είναι τα 3 μόνα τους αυτοκόλλητα που αγόρασε η Στέλλα.
Τον διαβάζουμε λοιπόν αυτόν τον αριθμό, 1 και 23 εκατοστά.
Ή 1,23.
Πάμε να δούμε τη μονάδα μας.
Η μονάδα μπορεί να είναι το οτιδήποτε.
Εδώ έχουμε 1 μονάδα, ένα τετράγωνο. Σαν το τετράγωνο με τα αυτοκόλλητα που αγόρασαν τα παιδιά.
Ένα ολόκληρο τετράγωνο είναι η μονάδα μας.
Μπορούμε να το χωρίσουμε σε 10 κομμάτια. 10/10 δηλαδή.
Και μπορούμε να το χωρίσουμε επίσης σε 100 κομμάτια, 100 διαφορετικά αυτοκόλλητα είχε πάνω του το τετράγωνο.
1 μονάδα λοιπόν είναι ισοδύναμη με 10 δέκατα ή 100 εκατοστά.
Μπορούμε να γράψουμε, όπως βλέπουμε ότι τα 10/10 είναι ισοδύναμα με τα 100/100,
δεκαδικούς αριθμούς που να γράφονται διαφορετικά, αλλά να είναι ισοδύναμοι;
Να είναι ακριβώς ίσοι;
Για να δούμε. Αυτό θέλουν να κάνουν η Ηρώ και ο Νικήτας.
Ο Νικήτας έχει ζωγραφίσει έναν δεκαδικό αριθμό. Μας δείχνει στο τετράγωνό του έναν δεκαδικό αριθμό.
Έχει χρωματίσει τα 30 τετραγωνάκια από τα 100.
Αν δείτε, είναι 3 τετραγωνάκια επάνω επί δέκα. Είμαι σίγουρη ότι είστε σαΐνια στην προπαίδεια, την έχετε μάθει από πέρσι.
30 τετραγωνάκια δηλαδή.
30 από τα εκατό είναι τα 30 εκατοστά.
Η Ηρώ θέλει να φτιάξει έναν αριθμό που να έχει ακριβώς την ίδια αξία με του Νικήτα.
Το δικό της τετράγωνο είναι χωρισμένο σε δέκατα.
10 λωρίδες. Κάθε μία από αυτές είναι το ένα δέκατο (1/10).
Παρατηρεί το τετράγωνο του Νικήτα και λέει: Εγώ θα χρωματίσω τις 3 λωρίδες,
τα 3 δέκατα (3/10).
Και τα χρωματίζει.
Και βλέπουμε ότι ο αριθμός του Νικήτα, τα 30/100, είναι ισοδύναμος με τον αριθμό που έφτιαξε η Ηρώ.
Η Ηρώ χρωμάτισε τα 3 από τα 10 ίσα κομμάτια, τα 3/10, δηλαδή, του τετραγώνου...
που είναι το 0,3.
Για να δούμε πώς θα βάλουμε αυτούς τους αριθμούς στην αριθμογραμμή!
Τα 30 εκατοστά του Νικήτα, 0, 30 ισοδυναμεί με 0,3. Τα τρία δέκατα της Ηρούς.
Άραγε αν είχαμε τον αριθμό 0,03 θα ήταν ίσος κι αυτός;
Για πάμε να δούμε που θα τοποθετήσουμε αυτούς τους αριθμούς σε μια αριθμογραμμή.
Έχω εδώ μια μεγάλη αριθμογραμμή. Εδώ βάζουμε το μηδέν.
Και κάπου εδώ θα βάλουμε το 1.
Τα βάζω σε μεγάλη απόσταση μεταξύ τους, για να μπορέσω να χωρίσω τη μονάδα μου σε δέκα δέκατα,
και να βλέπω και τα εκατοστά.
Αφού λοιπόν έχω χωρίσει τη γραμμή μου...
σε δέκα ίσα κομμάτια. 10 δέκατα.
Πάμε λοιπόν!
Εδώ είναι το πρώτο δέκατο, 0,1. 2 δέκατα, 3 δέκατα, 4 δέκατα και 0,5 στη μέση.
Και ούτω καθεξής. Και φτάνουμε στο 1, στη μια μονάδα.
Αν θέλουμε να βάλουμε τα 3 δέκατα της Ηρούς, μπορούμε κατευθείαν να πούμε ότι τα 3/10 είναι εδώ.
Τα 30 εκατοστά του Νικήτα, άραγε, πού πέφτουν;
Προφανώς πέφτουν κι αυτά εδώ, αφού κάθε δέκατο...
μπορούμε να το χωρίσουμε σε δέκα ίσα κομματάκια...
κι έτσι να έχουμε 100 τέτοια κομματάκια στη μονάδα μας. Εκατό εκατοστά.
Εδώ λοιπόν είναι τα 3 δέκατα αλλά και τα 30 εκατοστά.
Τα 3 εκατοστά που είναι; 3 εκατοστά, τι σημαίνει;
Έχω ακέραιες μονάδες; Μηδέν!
Έχω δέκατα; Μηδέν και στα δέκατα.
Έχω όμως 3 εκατοστά.
Πάω λοπόν στην αρχή της αριθμογραμμής μου, πολύ κοντά στο μηδέν,
και μετράω 3 από τις μικρές γραμμούλες.
Κάπου εδώ είναι: 0 οι ακέραιες μονάδες, 0 τα δέκατα. Δεν έχω φτάσει ακόμα στο δέκατο.
Και 3 εκατοστά.
Έτσι βλέπουμε στην αριθμογραμμή ότι το 0,03, τα 3 εκατοστά...
είναι άλλος αριθμός από τα 3 δέκατα, που είναι 30 εκατοστά.
Αυτό που πρέπει να θυμάστε είναι ότι σε έναν δεκαδικό αριθμό, μπορώ...
στο δεκαδικό κομμάτι, μετά το τελευταίο ψηφίο, να βάλω όσα μηδενικά θέλω, χωρίς να αλλάξει η αξία του.
Θα μπορούσα εδώ, στο 0,3 να βάλω πολλά μηδενικά ακόμα. Δεν αλλάζει η αξία του αριθμού αν βάλουμε μηδενικά.
Προσοχή όμως! Πού θα τα βάλουμε;
Μετά την υποδιαστολή, μετά το τελευταίο ψηφίο των δεκαδικών.
Πάμε τώρα να συνοψίσουμε αυτά που πρέπει να θυμόμαστε.
Οι δεκαδικοί αριθμοί μάς χρειάζονται και τους χρησιμοποιούμε καθημερινά στη ζωή μας.
Τους χρησιμοποιούμε για μετρήσεις.
Για να μετράμε μήκος, χρήματα, μάζα.
Μετράμε, γενικώς!
Χωρίζεται ένας δεκαδικός αριθμός, στο ακέραιο κομμάτι, και στο δεκαδικό.
Ανάμεσά τους πάντα υπάρχει μια υποδιαστολή,
ένα κόμμα.
Μια ακέραια μονάδα, ένα ολόκληρο, ισούται με 10 δέκατα ή με 100 εκατοστά.
Μην σας κουράσω άλλο για σήμερα.
Ελπίζω να είστε καλά, μέχρι την επόμενη φορά που θα τα ξαναπούμε!
Καλή συνέχεια!