Hareket imkansızdır! Zeno Paradoksu ||Zeno|paradoxe Bewegung ist unmöglich! Zenos Paradoxon Movement is impossible! Zeno's Paradox Le mouvement est impossible ! Paradoxe de Zeno Beweging is onmogelijk! Zeno's Paradox O movimento é impossível! Paradoxo de Zeno Движение невозможно! Парадокс Зенона

Hareket etmenin imkansız olduğunu biliyor muydunuz? Wussten Sie, dass es unmöglich ist, sich zu bewegen? Did you know that moving is impossible? Знаете ли вы, что двигаться невозможно? Bu videoyu sonuna kadar izledikten sonra öğrenmiş olacaksınız. Wenn Sie sich dieses Video bis zum Ende angesehen haben, werden Sie etwas gelernt haben. Bir başka deyişle okula ya da işe geç kaldığınızda artık son derece mantıklı bir mazeretiniz olacak. ||||||||vous arrivez||||||excuse| Mit anderen Worten: Sie haben jetzt eine vernünftige Entschuldigung, wenn Sie zu spät zur Schule oder zur Arbeit kommen. In other words, you will now have a perfectly reasonable excuse for being late for school or work. Другими словами, когда вы опаздываете в школу или на работу, теперь у вас будет вполне логичное оправдание. Evet bütün üşengeçler, ağır kanlılar, size sesleniyorum! ||paresseux||sanguins||j'appelle Ja, ihr faulen, schwerfälligen Menschen, ich rede mit euch! Yes, all lazy, heavy-blooded ones, I call you! Да, все ленивые, тяжелокровные, взываю к вам! Şimdi sesi açın ve ekrana bütün dikkatinizi verin. Schalten Sie nun den Ton ein und richten Sie Ihre Aufmerksamkeit auf den Bildschirm. Now turn up the volume and give the screen your full attention. Теперь увеличьте громкость и полностью сосредоточьтесь на экране.

Bir yerden bir yere gitmek her gün her zaman yaptığımız bir şey değil mi? Von einem Ort zum anderen zu gehen ist etwas, das wir jeden Tag tun, nicht wahr? Getting from place to place is something we do all the time, every day, right? Перемещаться с места на место — это то, чем мы занимаемся все время, каждый день, верно? Mesela okula, işe ya da markete alışveriş yapmaya her gün gidiyoruz. Wir gehen zum Beispiel jeden Tag zur Schule, zur Arbeit oder zum Einkaufen. Hatta evin içinde bile susadığımızda ya da televizyon izlemek istediğimizde hareket etmiş oluyoruz. ||||quand nous avons soif|||||||| Sogar innerhalb des Hauses bewegen wir uns, wenn wir Durst haben oder fernsehen wollen. Yürümek… Bir vasıtayla bir yerden bir yere gitmek… Hepsi bir şekilde hareket etmek anlamına geliyor. ||moyen de transport|||||||||||| Zu Fuß gehen... Mit einem Fahrzeug von einem Ort zum anderen fahren... Alle bedeuten, sich in irgendeiner Weise zu bewegen. Elimizi alnımıza götürdüğümüzde elimiz hareket ediyor. |à notre front|lorsque nous mettons|main|| Wenn wir unsere Hand an die Stirn legen, bewegt sich unsere Hand. When we bring our hand to our forehead, our hand moves. Gözlerimizi sağa sola çevirdiğimizde gözlerimiz hareket ediyor. |||lorsque||| When we turn our eyes to the right and left, our eyes move. Her şey hareket ediyor… Mu acaba? Everything is moving… Is it? Все движется… не так ли?

Şimdi gelin şöyle bir deney yapalım: Şu önümdeki ağaç hemen hemen benden on metre uzaklıkta. Now let's do an experiment: That tree in front of me is almost ten meters away from me. Теперь давайте проведем эксперимент: это дерево передо мной находится почти в десяти метрах от меня. Şimdi ağaca doğru yürümeye başladığımda yolun yarısına kadar kaç saniye zaman aldığını ölçeceğim. ||||||||||||je mesurerai Wenn ich nun anfange, auf den Baum zuzugehen, messe ich, wie viele Sekunden es dauert, bis ich die Hälfte des Weges geschafft habe. Теперь, когда я начну идти к дереву, я буду измерять, сколько секунд потребуется, чтобы пройти половину пути. Yolun yarısını oraya yerleştirdiğim kırmızı topla belirttim. |||a placé||balle|j'ai indiqué Ich habe die Hälfte des Weges mit dem roten Ball markiert, den ich dort platziert habe. Половину пути я отметил красным шариком, который поставил туда.

Evet şu an yolun tam yarısına geldim. Kronometrem bana 5 saniye zaman geçtiğini söylüyor. mon chronomètre||||| Pekala şimdi ağaca doğru yürümeye devam edeceğim. In Ordnung, ich gehe weiter auf den Baum zu. Хорошо, теперь я собираюсь продолжить идти к дереву. Şu an ağaçla aramızdaki mesafenin tam ortasında bir oyuncak araba var. Right now there is a toy car in the middle of the distance between us and the tree. Прямо сейчас на середине расстояния между нами и деревом стоит игрушечная машинка. Yürüyorum ve oyuncak arabanın yanına geldiğimde kronometreme bakıyorum. ||||||mon chronomètre| Я иду и смотрю на свой секундомер, когда добираюсь до игрушечной машинки. Kronometre bu kez iki buçuk saniye geçtiğini gösteriyor. le chronomètre||||||| Pekala devam ediyorum o halde. Bu kez ağaçla aradaki yolumun yarı mesafesine bir elma koydum. На этот раз я положил яблоко на полпути между моей дорожкой и деревом. Hop kronometreye bakıyorum; tam bir nokta üç saniye. |au chronomètre|||||| Хоп, я смотрю на секундомер; одна полная точка три секунды. Ağaca henüz varmadım. ||je suis arrivé I haven't reached the tree yet. Я еще не добрался до дерева. Ve yolun yarısına her varışımda bir miktar zaman harcamam gerekti. ||||arrivée||||dépenser| Und jedes Mal, wenn ich die Hälfte der Strecke geschafft hatte, musste ich etwas Zeit investieren. And every time I got halfway down I had to spend some time. И каждый раз, когда я спускался на полпути, мне приходилось тратить некоторое время. Yani ilk seferinde beş saniye sonra iki buçuk saniye şimdi de bir nokta üç saniye. Так что в первый раз это пять секунд, потом две с половиной секунды, теперь одна и три секунды. Benim kronometreye basma zamanım ve kusursuz bir zamanlama yapamadığım için bir nokta yirmi beş saniye geçmiş olması gerekiyordu ama ben bir nokta üç saniye ölçtüm, olsun sorun değil. ||pression||||||que je n'ai pas pu||||||||||||||||ai mesuré||| Настало мое время включить секундомер, и поскольку я не мог точно рассчитать время, одна точка должна была пройти за двадцать пять секунд, но я измерил одну целую три секунды, все в порядке. Bir nokta yirmi beş kabul edelim. Допустим, одна точка двадцать пять.

Şimdi soru şu: Ağaca kadar olan yolu yürürken arada kalan mesafenin her seferinde yarısına varabilmek için bir miktar zaman harcamam gerekti. ||||||||||||||atteindre|||||| Теперь вопрос: мне пришлось потратить некоторое время, идя по тропинке к дереву, чтобы каждый раз преодолевать половину расстояния. Bu bir miktar konusuna dikkatinizi çekmek istiyorum. I would like to draw your attention to this issue of quantity. Я хотел бы обратить ваше внимание на вопрос количества. Ne kadar zaman geçtiği o kadar önemli değil. Неважно, сколько времени прошло. Normal olarak hızlı yürürsem daha kısa zaman geçer, yavaş yürürsem uzun zaman geçer. |||je marche||||||||| Обычно, если я иду быстро, это занимает меньше времени, если я иду медленно, это занимает больше времени. Ama sonuç olarak bir miktar zaman mutlaka geçecek. Aber dadurch wird sicherlich einige Zeit vergehen. Но в результате какое-то время обязательно пройдет. Değil mi? İçinizde ‘ee ne var bunda?' Вы такой: «Ну, что в этом такого?» diyenler vardır. Ama eminim içinizde ‘bir saniye neler oluyor?' Но я уверен, что вы думаете: «Подождите секунду, что происходит?» diyen birileri de mutlaka vardır! Наверняка есть те, кто говорят! Böyle insanlar binlerce yıldır var. Такие люди существуют тысячи лет.

Bundan yaklaşık iki bin beş yüz yıl önce, yani meşhur Sokrates'ten de önce bugünkü İtalya'nın güney batı kıyısındaki bir kasabada doğmuş huysuz bir adam vardı. ||||||||||Socrate||||d'Italie|||sur la côte de||||grincheux||| Vor etwa zweitausendfünfhundert Jahren, noch vor dem berühmten Sokrates, wurde in einer Stadt an der Südwestküste des heutigen Italiens ein mürrischer Mann geboren. Около двух тысяч пятисот лет назад, еще до знаменитого Сократа, в городке на юго-западном побережье сегодняшней Италии родился угрюмый человек. Bu huysuz ihtiyar bir gün evine giderken benim az önce yaptığım şeyi yaptı ve dedi ki; ||vieux||||||||||||| Этот ворчливый старик сделал то же, что и я, когда однажды возвращался домой, и сказал:

“Arkadaş bir dakika ya ne oluyor burada! "Wait a minute, friend, what's going on here! «Подожди, друг, что тут происходит! Ben yolun her yarısına gelişimde bir miktar zaman harcıyorsam ve her seferinde önümde yine yolun yarısı varsa… bu kadar zamanı toplarsam ben eve hiç varamayacağım galiba!” ||||développement||||||||devant moi||||||||si je cumule||||n'arriverai| Wenn ich jedes Mal, wenn ich die Hälfte des Weges zurückgelegt habe, eine bestimmte Zeit verbringe, und jedes Mal gibt es eine weitere Hälfte des Weges... wenn ich so viel Zeit zusammenzähle, komme ich wahrscheinlich nie zu Hause an!" Если я трачу какое-то время на дорогу к каждой половине дороги, и каждый раз передо мной еще половина дороги… если я соберу столько времени, я думаю, я никогда не доберусь до дома!»

Evet, zaman her yarı yolda gittikçe azalıyor, yani mesafe kısaldığı için her seferinde daha az zaman geçiyor ama sonuçta üç beş bir miktar zaman geçiyor. |||||||||se raccourcit||||||||||||||| Да, время становится короче с каждой половиной пути, поэтому с каждым разом проходит все меньше времени по мере того, как расстояние становится короче, но в итоге проходит три или пять раз. Ve işte bu bütün üç beşleri toplaya toplaya sonsuza kadar sonsuz zaman geçmesi gerekecek! |||||cinq|||||||passage| Und es wird unendlich lange dauern, all diese drei Fünfer zusammenzuzählen! И складывать все эти три пятерки придется целую вечность! Gidilecek yer neresi olursa olsun, eğer sonsuz zaman geçmesi gerekecekse… O zaman hareket etmek imkansızdır! à aller|||||||||il faudra||||| Где бы ни был пункт назначения, если должно пройти бесконечное время… Тогда двигаться невозможно!

Bu argümanı mantık çerçevesinde ele alacak olursak: |argument||||| Wenn wir dieses Argument logisch betrachten: Si nous considérons cet argument dans le cadre de la logique : Если рассматривать этот аргумент логически:

Hareket bir süper görevdir, çünkü belirlenmiş herhangi bir mesafe boyunca hareketin tamamlanması sonsuz sayıda adım içerir, Süper görevler imkansızdır, Bu nedenle hareket de imkansızdır. ||||||||||||||étape|||tâches|||||| Le mouvement est une super tâche, car l'achèvement du mouvement sur n'importe quelle distance déterminée implique une infinité d'étapes. Les super tâches sont impossibles, donc le mouvement est également impossible. Движение — это сверхзадача, потому что для совершения движения на любое заданное расстояние требуется бесконечное количество шагов, Сверхзадачи невозможны, следовательно, и движение невозможно. İşte Elealı Zeno'nun ortaya attığı bu paradoks matematik tarihinin en büyük tartışma konularından biri oldu ve inanmayacaksınız bugüne kadar güncelliğini korudu. ||||lancé||||||||parmi des sujets||||vous ne croirez|||actualité|a maintenu Dieses von Zenon von Elea aufgestellte Paradoxon wurde zu einer der größten Debatten in der Geschichte der Mathematik, und, Sie werden es nicht glauben, es ist bis heute aktuell geblieben. Voici le paradoxe soulevé par Zénon d'Élée qui est devenu l'un des plus grands sujets de débat dans l'histoire des mathématiques, et vous ne le croirez pas, il reste d'actualité jusqu'à aujourd'hui. Zeno'nun çağdaşı düşünürler, matematikçiler kendilerince cevaplar verdi. |contemporain||les mathématiciens||| Bilim ve düşünce dünyasının en büyük zihinleri bu problemi çözebilmek için çaba sarfetti. ||||||esprits|||pouvoir résoudre|||a fourni Die größten Köpfe der Wissenschaft und des Denkens haben sich bemüht, dieses Problem zu lösen.

Einstein'ın hayali yeğeni bile bir filmde bu paradoksu kullandı. ||neveu|||||| Hem de çok zekice bir yerde… |||intelligemment|| Und das an einem sehr klugen Ort.

Sanırım amcan dans etmemizi istiyor. |ton oncle||| Я думаю, твой дядя хочет, чтобы мы потанцевали. Alakası yok Ed, oradan buraya atlayamazsın. ||Ed|||tu ne peux pas sauter Das ist irrelevant, Ed, du kannst nicht einfach von hier nach dort springen. It's okay, Ed, you can't jump around. Neden olmasın? Senin gibi parlak ve ünlü bir bilim adamının Zeno'nun paradoksundan habersiz olduğunu söyleme bana. |||||||||paradoxe|inconscient||| Не говорите мне, что такой блестящий и известный ученый, как вы, не знает о парадоксе Зенона. Hatırlat. rappelle Remind me.

O hatırlatmadan önce bu paradoksu çözmeye çalışan ünlü bir kaç isimden bahsedelim. |sans rappeler|||||||||| Bevor wir ihn daran erinnern, wollen wir über ein paar berühmte Namen sprechen, die versucht haben, dieses Paradoxon zu lösen. Mesela Sinoplu Diyojen'den. |de Sinop|de Diogène Diogenes von Sinope, zum Beispiel. Hani şu Büyük İskender'e posta koyan yürek yemiş düşünür. où|||à Alexandre|poste|a osé|courage|fruit| Sie wissen schon, der herzlose Philosoph, der es mit Alexander dem Großen aufnahm. You know, the one who put mail to Alexander the Great thinks heartbroken. Eh bien, c'est le penseur audacieux qui défie le grand Alexandre. Вы знаете, тот, кто отправил почту Александру Македонскому, думает, что у него разбито сердце. Kendisine bu paradokstan bahsettiklerinde karadenizlilere özgü pratik zekasıyla dedi ki “Bunu çözmek yerine Zeno'nun yanıldığını gösteririm.” Yerinden kalktı ve yürüyerek hareket etmenin imkansız olmadığını gösterdi. |||lorsqu'ils en parlaient||propre|||||||||il était|||||||||| Als man ihm von diesem Paradoxon erzählte, sagte er mit der für die Schwarzmeerbewohner typischen praktischen Intelligenz: "Anstatt es zu lösen, werde ich zeigen, dass Zeno sich geirrt hat", stand von seinem Sitz auf und zeigte, dass es nicht unmöglich war, sich zu Fuß fortzubewegen. Lorsque les gens lui parlèrent de ce paradoxe, il dit avec l'intelligence pratique typique des gens de la mer Noire : "Au lieu de résoudre cela, je vais montrer que Zeno s'est trompé." Il se leva et démontra que se déplacer n'était pas impossible. Когда ему рассказали об этом парадоксе, он со своей черноморской изобретательностью сказал: «Вместо того, чтобы решить его, я покажу Зенону неправоту». Он встал и показал, что можно передвигаться пешком. Meşhur Aristo, Zeno'nun ortaya attığı hemen hemen bütün paradokslara şüpheci yaklaştı ve bu problemde yarı yolu kat etmek için geçen zamanın da azalmasından yola çıkarak her halükarda varış noktasına varıldığını iddia etti. ||||||||paradoxes|sceptique||||dans ce problème|||||||||||||dans tous les cas|arrivée||varıldığını|| Der berühmte Aristoteles stand fast allen Paradoxien Zenos skeptisch gegenüber, und in diesem Fall behauptete er, dass das Ziel auf jeden Fall erreicht sei, da die Zeit, die man für die Hälfte des Weges benötigt, ebenfalls abnimmt. Le célèbre Aristote aborda presque tous les paradoxes soulevés par Zeno avec skepticism et affirma qu'on atteignait de toute façon le point d'arrivée, en se basant sur la réduction du temps nécessaire pour parcourir la moitié du chemin dans ce problème. Знаменитый Аристотель скептически относился почти ко всем парадоксам, поднятым Зеноном, и утверждал, что пункт назначения в любом случае достигнут, исходя из сокращения времени, необходимого для решения этой проблемы наполовину. Aristo bu problemde bölünebilirlik fikri üzerinde de kafa yormuştu. |||divisibilité|||||avait réfléchi Aristoteles hat bei diesem Problem auch über die Idee der Teilbarkeit nachgedacht. Аристотель также размышлял над идеей делимости в этой проблеме. Neyi nereye kadar bölebiliyoruz? |||pouvons-nous diviser Wie weit können wir was einteilen? How far can we divide what? Как далеко мы можем разделить что? Zaman ne kadar bölünebilir? |||peut être divisé Wie teilbar ist die Zeit? How can time be divided? Mesafe ne kadar bölünebilir? How much can the distance be divided?

Bütün zamanların en büyük üç matematikçisinden biri olarak kabul edilen Arşimet ise haliyle matematiksel bir çözüm önerdi. |des temps||||matématicien|||||||||||a proposé Archimedes, der als einer der drei größten Mathematiker aller Zeiten gilt, schlug eine mathematische Lösung vor. Archimedes, considered one of the three greatest mathematicians of all time, naturally offered a mathematical solution. Düzgün olmayan bir şeklin alanını hesaplamak için geliştirdiği yöntemle aynı yöntemi kullanarak gittikçe azalan kesirlerin toplamının sonlu bir sayı olduğunu kanıtladı. |||||calculer||||||||décroissant|des fractions||fini||||a prouvé Using the same method he developed to calculate the area of an irregular shape, he proved that the sum of progressively decreasing fractions is a finite number. Arşimet gerçekten büyük bir matematikçiydi çünkü bugünkü bilgimizle bizler de onun vardığı sonuçların aynısına varıyoruz. |||||||notre connaissance|||||résultats|identiques|parvenons Archimedes war in der Tat ein großer Mathematiker, denn mit unserem heutigen Wissen kommen wir zu denselben Schlussfolgerungen wie er. Archimedes was indeed a great mathematician, because with our current knowledge we arrive at the same conclusions as he did.

Zeno'nun ortaya attığı diğer paradokslar da benzer çelişkiler üzerine kuruluydu. ||||paradoxes|||contradictions||était établi Andere von Zeno vorgeschlagene Paradoxa beruhen auf ähnlichen Widersprüchen. Other paradoxes that Zeno put forward were based on similar contradictions. Mesela; Akhilleus ve kaplumbağanın yarışı. |Achille|||

Antik çağların efsane savaşçısı Akhilleus ile kaplumbağa yarışmaya karar verirler. |des âges|légende|guerrier||||à la course|| The tortoise decides to compete with Achilles, the legendary warrior of ancient times. Ancak yiğit ve alicenap Akhilleus kaplumbağaya bir imtiyaz tanır. |brave||généreux||à la tortue||privilège| Doch der tapfere und barmherzige Achilles macht der Schildkröte ein Zugeständnis. However, the valiant and gracious Achilles grants a privilege to the tortoise. Kaplumbağanın yarışa yolun yarısından itibaren başlamasına izin verir. |course||||de commencer|| Erlaubt der Schildkröte, das Rennen nach der Hälfte der Zeit zu beginnen. Allows the turtle to start the race halfway down the road.

Huysuz ihtiyar Zeno tam burada yine araya girer! Grumpy old Zeno interrupts right here again!

Yarış başladığında Akhilleus yolun yarısına yani kaplumbağanın yarışa başladığı noktaya geldiğinde, kaplumbağa da kendi önündeki yolun yarısına gelmiş olsun. Yarış böyle devam edecek olursa ne kaplumbağa ne de Akhilleus bitiş noktasına varamayacakları gibi, Akhilleus da hiçbir zaman kaplumbağayı yakalayamayacak demektir! ||||||||||fin||n'arriveront|||||||attraper| Koskoca Akhilleus. Huge Achilles. Kaplumbağayı! Hadi ordan! Get out of there!

Ya da bir başka paradoks: Yayından çıkmış bir ok düşünün. |||||de l'arc|||| Oder ein anderes Paradoxon: Stellen Sie sich einen Pfeil vor, der von seinem Bogen abgeschossen wird. Or another paradox: Think of an arrow out of a bow. Bu okun havadayken hareketsiz olduğu bir an vardır. |flèche||immobile|||| There is a moment when this arrow is motionless while in the air. Değil mi? Öyle küçük bir an olsun ki bu, ok o an hareketsiz olsun. Let it be such a small moment that the arrow is still in that moment. İyi ama böyle bir an varsa ok diğer bütün anlarda da hareketsizdir. |||||||||moments||est immobile Aber wenn es einen solchen Moment gibt, ist der Pfeil in allen anderen Momenten unbeweglich. Good, but if there is such a moment, the arrow is at rest at all other moments as well. Öyleyse ok hiçbir zaman hareketli olamaz. So the arrow can never be in motion.

Peki şuna ne demeli? Was ist mit dem hier? Yan yana üç tane tren rayı üzerinde üç tane vagon olsun. |||||rails||||| Es seien drei Waggons auf drei nebeneinander liegenden Gleisen. Let there be three wagons on three train tracks side by side. Her vagonun üçer tane penceresi olsun. |wagon|trois||| Jeder Wagen soll drei Fenster haben. Siz ortadaki vagonun ilk penceresinin yanında oturuyorsunuz. ||||fenêtre||vous êtes assis Birinci tren sola doğru hareket ediyor olsun. Der erste Zug soll nach links fahren. Diğer tren ise aynı yönde iki kat hızlı gidiyor olsun. Siz bu durumda kendi hızınızın ne olduğunu asla öğrenemeyeceksiniz demektir. ||||vitesse||||vous n'apprendrez| Bu paradoks aslında bize hareket dediğimiz şeyi tanımlayabilmek için sabit kabul edeceğimiz bir şeye, bir referansa ihtiyaç duyduğumuzu anlatır. |||||||pouvoir définir||||||||référence||nous avons besoin| This paradox actually tells us that we need something that we can accept as a constant, a reference, in order to define what we call movement.

Arşimetten bu yana çok sayıda matematikçi bu paradokslarla ilgili kafa yordu. d'Archimède||||nombre|||paradoxes|||a réfléchi Seit Archimedes haben viele Mathematiker über diese Paradoxa gerätselt. Aslında konu benim videonun başında varmaya çalıştığım ağaca varıp varamama konusundan çok daha derin. |||||arriver||||arriver|sujet||| Tatsächlich geht es um viel mehr als darum, ob ich den Baum, den ich zu Beginn des Videos erreichen wollte, erreichen kann oder nicht. In fact, the issue is much deeper than whether I can reach the tree I tried to reach at the beginning of the video. Yani ağaca varmak mesele değil. Zor olan kısım bu değil. That's not the hard part. Mesele çook daha derin. |très|| The issue is much deeper.

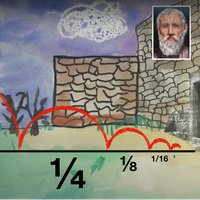
Önce ‘kolay' dediğim şeyi açıklamaya çalışayım: Bir kenarı bir metre uzunluğunda bir kare çizelim. |côté||||||tracons Zeichne ein Quadrat mit einer Seitenlänge von einem Meter. Bu kareyi ortadan ikiye bölersek karenin alanının yarısını elde ederiz. ||||si nous divisons|du carré|||| If we divide this square in half, we get half the area of the square. Bu yarım karelerden birini yine ikiye bölersek dörtte bir kare elde etmiş oluruz. ||carrés|||||||||| Wenn wir eines dieser halben Quadrate noch einmal in der Hälfte teilen, erhalten wir ein Viertelquadrat. If we divide one of these half squares into two again, we get a quarter square. Bu şekilde devam ederek

½ + ¼ + ⅛ + 1/16 + 1/32 … şeklinde sonsuza kadar toplayacak olsak aslında sonsuz bir alan elde etmeyeceğimizi görebiliyoruz. ||||||||||nous n'obtiendrons| Wenn wir ½ + ¼ + ⅛ + 1/16 + 1/32 ... unendlich addieren würden, könnten wir sehen, dass wir nicht wirklich eine unendliche Fläche erhalten würden. Elde edeceğimiz alan en başta elimizdeki bir metreye bir metre kareden başka bir şey olmayacaktır. ||||||||||de mètre carré|||| Die Fläche, die wir erhalten werden, wird nicht größer sein als das Quadrat von einem Meter mal einem Meter, das wir ursprünglich hatten. İhtiyar Zeno'nun paradoksunun matematiksel çözümünü bulduk. ||paradoxe||| Wir haben die mathematische Lösung des alten Paradoxons von Zeno gefunden. We found the mathematical solution to old Zeno's paradox. Rahatladık mı? nous sommes rassurés| Are we relaxed? Hayır.

Alman matematikçi Herman Weyl paradoksu kökten çözmek için bir yol aramış ve demiş ki “Madem öyledir, ha bu çainat sonsuza kadar bölünemiyor olmasın da?” Ehm. ||Herman|Weyl||radicalement|||||a cherché||||puisque||||univers|||divisible|||Euh Der deutsche Mathematiker Hermann Weyl suchte nach einer Möglichkeit, das Paradoxon radikal zu lösen, und sagte: "Wenn das so ist, warum kann das Universum nicht unendlich geteilt werden?" Ehm. Pardon o başkasıydı, Herman Weyl demiş ki, birbirinden farklı iki nokta arasında her zaman bir başka nokta olduğu fikrini reddedersek problem çözülür. ||était|||||||||||||||||si nous rejetons||est résolu Entschuldigung, das war jemand anderes. Hermann Weyl sagte, dass das Problem gelöst ist, wenn wir die Vorstellung ablehnen, dass es zwischen zwei verschiedenen Punkten immer einen weiteren Punkt gibt. Yani ağaca doğru yürürken her zaman önünde yolun yarısı kadar bir mesafe olduğunu söylemiştim ya… Öyle bir nokta vardır ki diyor Herman Weyl, artık önünüzde yolun başka yarısı kalmamıştır. Bir nokta sonra doğrudan ağaca varabilirsiniz. |||||vous pouvez arriver After a point, you can reach the tree directly.

Herman Weyl modern fizikçilerin uzay-zaman adını verdikleri evrenin yapısını sorgulamış ve sürekli sonsuza kadar bölünebilen bir evrende yaşadığımız fikrinin yerine süreksiz ve kesintili bir evrende yaşadığımız fikrini önermiştir. |||des physiciens|||||||a interrogé|||||divisible||||||discontinu (1)||discontinu|||||a proposé

Ama bir saniye! Eğer öyleyse… Ben en dibine kadar indiğim o noktadan bir diğer noktaya giderken… resmen… ışınlanmış oluyorum! ||||au fond||je descends||||||||téléporté| Wenn ja... wenn ich von diesem Punkt zu einem anderen Punkt gehe, von dem aus ich ganz nach unten gestiegen bin... werde ich buchstäblich... teleportiert! If so… I am literally… teleported as I go from that very bottom point to another point… Öyle mi?

Buraya gelemezsin, kalan mesafenin yarısını aşman gerekir. |tu ne peux pas venir||||aşman(1)| Sie können nicht hierher kommen, Sie müssten die Hälfte der verbleibenden Strecke zurücklegen. Onun yarısını benim almam gerekir. |||achat| I have to take half of it. Sizce bu ikili ne zaman buluşurlar? |||||se rencontrent When do you think these two will meet?

Bu soruya yanıt olarak bir matematikçi asla buluşamayacaklarını söyler çünkü seriler sonsuz. |||||||ils ne pourront pas se rencontrer|||séries| In response to this question, a mathematician says they will never meet because the series are infinite.

Ancak kalanın yarısı hala orada, o mesafeyi almam gerekir ve… Bir fizikçi zaman sonsuzluğa eşit olduğunda buluşacaklarını söyler. |de la ville|||||distance|||||||à l'infini|||| But half of the rest is still there, I have to cover that distance and... A physicist says they will meet when time equals infinity.

…onun da hala yarısı kaldı, o mesafenin yarısını alırım, ve onun da yarısı Peki bir mühendis ne der? …that's still half of it, I'll take half that distance, and half that. So what does an engineer say? Bir dakika içinde tüm pratik amaçlar için yeterince yakın olacaklarını… In a minute they will be close enough for all practical purposes.

Gördüğünüz gibi ihtiyar Zeno 2500 yıl önce bir paradoks ortaya atmış, hala onu konuşuyoruz. As you can see, old Zeno came up with a paradox 2500 years ago and we are still talking about it. Çünkü Bertrand Russell'ın dediği gibi Zeno'nun argümanları, bir şekilde, zamanından günümüze kadar inşa edilmiş olan neredeyse tüm uzay, zaman ve sonsuzluk teorilerinin temelini oluşturmuştur. |Bertrand|||||arguments||||||||||||||l'infini|||a constitué Denn, wie Bertrand Russell sagte, bildeten Zenos Argumente irgendwie die Grundlage für fast alle Theorien über Raum, Zeit und Unendlichkeit, die seit seiner Zeit entwickelt wurden. Because, as Bertrand Russell said, Zeno's arguments somehow formed the basis for almost all the theories of space, time and infinity that have been constructed since his time. Russell'ın kasdettiği bu temel aslında “farklı düşünebilme becerisi.” Bir gün evine giderken ortaya attığı bu paradoksla “hareket etmek imkansızdır” gibi absürd bir sonuca varınca binlerce yıl insanların sonsuzluk kavramı hakkında düşünmesine yol açtı. |qu'il visait|||||capacité de penser|||||||||paradoxe|||||absurde|||arrivant||||||||| Als er mit diesem Paradoxon, das er sich eines Tages auf dem Heimweg ausgedacht hatte, zu der absurden Schlussfolgerung kam, dass "es unmöglich ist, sich zu bewegen", führte dies dazu, dass die Menschen Tausende von Jahren lang über das Konzept der Unendlichkeit nachdachten. What Russell meant by this foundation is actually "the ability to think differently." One day, on his way home, he came up with this paradox, which led to the absurd conclusion that "it is impossible to move" and led people to think about the concept of infinity for thousands of years. Bir mesafe sonsuza kadar bölünebilir mi? Bölünemezse en küçük mesafe nedir? si elle ne peut pas être divisée|||| What is the smallest distance if not divisible? Planck uzunluğu mu? Planck|| Planck length? Hareket etmek imkansız değilse bizim anladığımız anlamda sonsuzluk diye bir şey yok mu? |||||comprenons||||||| If movement is not impossible, is there no such thing as eternity as we understand it?