Rompecabezas 🍩 TOPOLÓGICO
¡Os propongo un rompecabezas topológico!
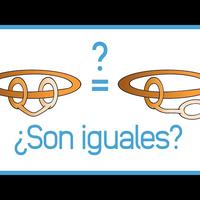
Consideremos los siguientes jueguetes A) y B) formados de goma.
Por un lado, tenemos un toro con un agujero. Vamos, un donut de toda la vida, junto a otro
toro con dos agujeros ambos enlazados al primero.
Y por otro lado tenemos un toro con un agujero junto a otro toro con dos agujeros, de forma
que tan solo uno de ellos está enlazado al primero.
¿SON IGUALES ESTOS DOS JUGUETES DE GOMA?
Seamos más precisos en la pregunta.
Debemos aclarar qué entendemos por “IGUAL”.
Ambos espacios A) y B) están encajados en el espacio euclídeo tridimensional.
Dado que nuestros espacios son de goma, nos preguntamos si podemos deformar, estirar,
encoger el espacio A) dentro de dicho espacio ambiente, siempre que no rasguemos ni peguemos
partes separadas, hasta convertirlo en el espacio B).
En este caso diremos que ambos encajes son ISOTÓPICOS.
¿Qué pensáis?
¿Podremos deformar la figura A) hasta convertirla en la figura B)?
En unos instantes lo sabremos ¡Empezamos!
Hemos planteado este acertijo en redes sociales y el 90% de las respuestas eran negativas.
El argumento para negar la existencia de la deformación es simple:
En A) podemos considerar como subespacio un par de anillos enlazados.
Sin embargo, tras liberar uno de los agujeros, en B) estos dos anillos estarían separado.
Y es claro que no podemos separar dos anillos enlazados sin ROMPERLOS.
Este argumento parece sólido.
¿Qué pensaríais si os dijera que la respuesta es que SI podemos deformar el espacio A) en
el espacio B)?
Quizás que me he vuelto loco, pero lo cierto es que los encajes A) y B) son en efecto,
ISOTÓPICOS.
¡Vamos a verlo! -Agrandamos el agujero que queremos liberar
-comprimimos las dos rosquillas -y empezamos a deformar la rosquilla grande
de forma que “rodeamos” a la pequeña a través del agujero del toro principal.
-Finalmente tenemos el agujero desenlazado como queríamos
Seguramente muchos de vosotros estaréis desconcertados y sospecháis que hay algún truco oculto
¿En qué falla el argumento de los dos anillos enlazados?
Para entender este misterio vamos a volver hacia atrás y repetir la deformación fijándonos
en cómo se deforma el anillo rojo.
El anillo rojo se deforma de tal manera que, tras desenlazar el agujero, permanece enlazado
al toro de un agujero, contrariamente a como creíamos.
Si te ha gustado el acertijo dale al Like y suscríbete.
Pronto volveremos con más acertijos sorprendentes.